Tobias's Blog

二叉树DFS、BFS、Morris遍历

数据结构与算法
Word count: 6.7kReading time: 28 min
2019/11/26 Share

序言

最近一个月时间都在集中刷leetcode的树部分的题目，发现解法普遍都可以用二叉树的各种遍历来解题，而且一道题有很多种解法。

我们在学习深度优先遍历和广度优先遍历时就知道，这两种遍历可以用在图和树中，其中树的DFS（深度优先遍历）分为前序、中序和后序三种，这三种方式可以用递归的方式或者用栈来迭代，也可以使用Morris算法来实现。

而BFS（广度优先遍历，相对简单很多）迭代整个树并用一个队列配合即可实现层级遍历

1574751742533

DFS

深度优先遍历，顾名思义，就是优先遍历整个树的深度，然后再遍历完整个树

深度优先遍历需要不断的往下递归遍历，而递归又涉及出栈和入栈的过程，所以三种DFS迭代的方式遍历我们都会使用一个Stack来模拟出栈和入栈的过程

分别可以用递归和迭代以及Morris算法来实现，Morris我们将放到最后再一起讲

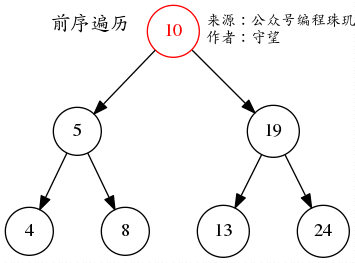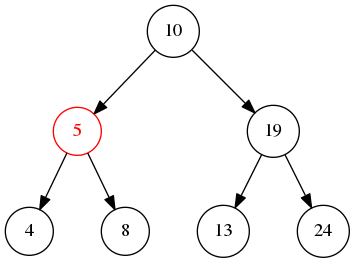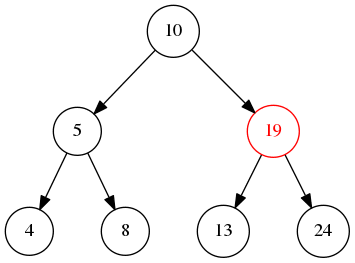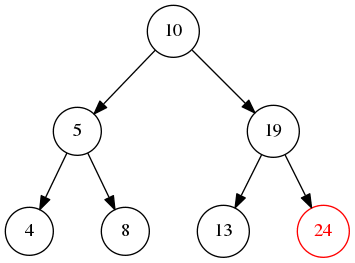
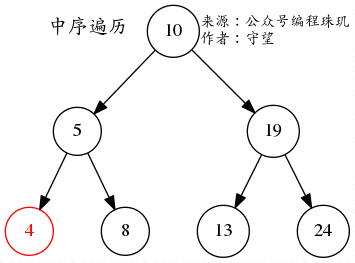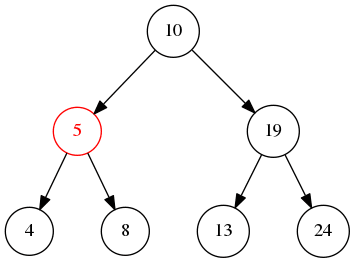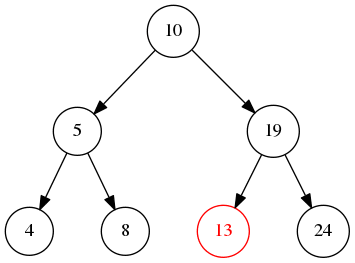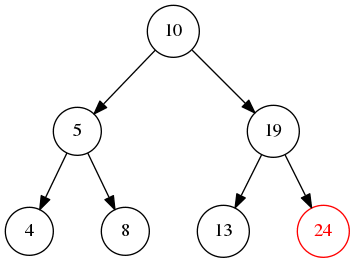
前序遍历

顾名思义就是先打印或检查当前节点，再不断的遍历左子树和右子树

1556505960888183

如图所示，从根节点不断的遍历左边直到叶子节点，然后再遍历右边，那么输出就是10->5->4->8->19->13->24

递归写法

那么上面说了是先打印当前节点再不断遍历左节点压栈，然后不断出栈，再遍历当前节点的右节点树，那么代码就很简单了

1
2
3
4
5
6
7
8
9
10
public void preOrderTraversalByRecursive(TreeNode root) {
    if (root != null) {
      // 打印当前节点
      System.out.println(root.val);
      // 递归左节点
      preOrderTraversalByRecursive(root.left);
      // 递归右节点
      preOrderTraversalByRecursive(root.right);
    }
  }

迭代写法

前面讲到需要不断的入栈和出栈，所以我们需要借助一个Stack来实现这个过程，先序遍历的迭代写法有两种，分别有两种特性。第一种会丢失掉右孩子，而第二种不会丢失

第一种，丢失右节点

因为不断的先将左孩子入栈，所以会丢失右孩子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public void preOrderTraversalByIteratorWithLossRightNode(TreeNode root) {
    if (root == null) {
      return;
    }
    Stack<TreeNode> stack = new Stack<>();

    while (root != null || !stack.isEmpty()) {
      if (root != null) {
        // 拿到当前节点，打印节点的值
        System.out.println(root.val);
        // 不断的入栈
        stack.push(root);
        // 将当前节点的左节点赋值为当前节点，不断的将左节点入栈
        root = root.left;
      } else {
        // 到达最左叶子节点，出栈然后将出栈节点的右节点赋值为当前节点
        // 例如：叶子节点为4：root = pop.right = null
        // 因为root = null,下一次还是继续出栈，这时候pop = 5，root = pop.right = 8，这时候8会被打印然后入栈并不断的遍历左节点
        TreeNode pop = stack.pop();
        root = pop.right;
      }
    }

  }

第二种，不丢失右节点

因为第一种是先不断的压栈左节点，没有保存右节点，导致的右节点丢失，所以第二种我们就可以提前将右孩子保存到栈中，就可以保证右节点不丢失了，同时利用栈的后入先出的特性就可以将右节点给压到栈底部

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public void preOrderTraversalByIteratorWithDoNotLoseRightNode(TreeNode root) {
    if (root == null) {
      return;
    }
    Stack<TreeNode> stack = new Stack<>();
    // 将根节点压栈
    stack.push(root);
    while (!stack.isEmpty()) {
      // 不断的出栈，栈的变化 第一次循环 10 ，然后出栈后栈为空，然后右和左节点压栈，栈：19，5，
      // 第二次 5 出栈，栈：19，然后再将右左入栈，栈：19，8，4
      // 第三次 4 出栈，栈：19， 8， 第四次 8 出栈， 栈：19
      // 第五次 19 出栈， 栈为空，然后24，13入栈，然后13和24在依次出栈
      TreeNode pop = stack.pop();
      // 打印出栈的当前节点
      System.out.println(pop.val);
      // 将出栈节点的右节点压栈
      if (pop.right != null) {
        stack.push(pop.right);
      }
      // 将左节点压栈
      if (pop.left != null) {
        stack.push(pop.left);
      }
    }
  }

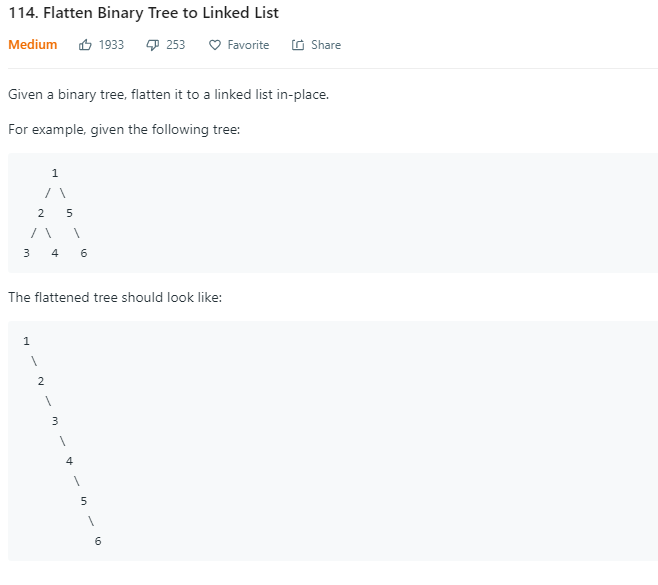
两种遍历在leetcode的应用

leetcode有一道题是将一个二叉树变成一条链表形式的二叉树114. Flatten Binary Tree to Linked List

1574821875748
因为第一种遍历会丢失右节点，所以我们需要不断的找出左子树最右边的节点一遍把右节点接过来

过程如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
1.将左子树插入到右子树的地方
2.将原来的右子树接到左子树的最右边节点
3.考虑新的右子树的根节点，一直重复上边的过程，直到新的右子树为 null
    
    1
   / \
  2   5
 / \   \
3   4   6

//将 1 的左子树插入到右子树的地方
    1
     \
      2         5
     / \         \
    3   4         6        
//将原来的右子树接到左子树的最右边节点
    1
     \
      2          
     / \          
    3   4  
         \
          5
           \
            6
 //将 2 的左子树插入到右子树的地方
    1
     \
      2          
       \          
        3       4  
                 \
                  5
                   \
                    6   

 //将原来的右子树接到左子树的最右边节点
    1
     \
      2          
       \          
        3      
         \
          4  
           \
            5
             \
              6         

  ......

代码 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public void flatten(TreeNode root) {
    while (root != null) { 
        //左子树为 null，直接考虑下一个节点
        if (root.left == null) {
            root = root.right;
        } else {
            // 找左子树最右边的节点
            TreeNode pre = root.left;
            while (pre.right != null) {
                pre = pre.right;
            } 
            //将原来的右子树接到左子树的最右边节点
            pre.right = root.right;
            // 将左子树插入到右子树的地方
            root.right = root.left;
            root.left = null;
            // 考虑下一个节点
            root = root.right;
        }
    }
}

第二种 我们用栈保存了右孩子，所以不需要担心右孩子丢失了。用一个 pre 变量保存上次遍历的节点，这样我们就不需要每次都去找左子树最右边的节点，时间复杂度因此也好减少，性能也会更好

过程 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
 root             last = null  stack={  1     }
    1                                  / \
   / \                                2   5
  2   5                              / \   \        
 / \   \                            3   4   6
3   4   6

将根节点出栈 
pop                 last = null  stack = {5    |     2  }
    1                                      \   |    / \
   / \                                      6  |   3   4
  2   5
 / \   \
3   4   6
然后将last = pop

下一次循环
pop       last      stack = {5   | 4 | 3}
  2        1                  \  |
 / \      / \                  6 |			
3   4    2   5
        / \   \
       3   4   6
这时候last不等于空了
将last的右边等于出栈节点然后断掉左节点
last
1
 \
  2
 / \
3   4
将pop赋值给last,移动到2节点
pop      last     stack = {5   | 4}
3         2                 \  |
         / \                 6 |
        3   4
然后pop赋值给last的右节点同时断开左节点
last
1
 \
  2
   \
    3
然后将pop赋值给last,移动到3节点，依次类推
pop  last  stack = 5
4    3              6
last
1
 \
  2
   \
    3
     \
      4
pop    last   stack = 6 
5       4
 6
last
1
 \
  2
   \
    3
     \
      4
       \
        5
................         
就这样不断的先序遍历来将出栈的节点赋值给last的右节点，同时不断的断开左节点，利用不会丢失右节点的先序遍历方式来实现

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public void flatten(TreeNode root) {
    if (root == null) {
      return null;
    }
    Stack<TreeNode> stack = new Stack<>();
    // 将根节点入栈
    stack.push(root);
    // 初始化上一个节点
    TreeNode last = null;
    while (!stack.isEmpty()) {
        
      TreeNode pop = stack.pop();
      if(last != null){
        // 将上一个节点的右节点赋值为当前出栈节点，并且断开左边的节点
        last.right = pop;
        last.left = null;
      }
      if (pop.right != null) {
        stack.push(pop.right);
      }
      if (pop.left != null) {
        stack.push(pop.left);
      }
      // 将当前节点赋值给last
      last = pop;
    }
  }

中序遍历

顾名思义就是先遍历左子树，然后检查当前节点值或打印输出，最后遍历右子树

由于二叉树定义，当前节点的左节点的值小于当前节点，右节点大于当前节点的问题，所以中序遍历会打印出从小打到右顺序的值。

在中序应用方面，通常我们可以利用这个特性来判断一个树是否符合二叉树的左节点小于根节点，右节点大于根节点，以及我们可以利用中序输出的结果加上前序或者后序的结果来还原一个完整的树

1556505961310255

先不断遍历左节点，直到最左边的叶子节点4，然后5出栈，再将5的右节点入栈，所以最后的结果是：4->5->8->10->13->19->24

递归写法

1
2
3
4
5
6
7
8
9
10
public void inOrderTraversalByRecursive(TreeNode root) {
    if (root != null) {
      // 递归左节点
      inOrderTraversalByRecursive(root.left);
      // 打印当前节点
      System.out.println(root.val);
      // 递归右节点
      inOrderTraversalByRecursive(root.right);
    }
  }

迭代写法

还是一样借助栈来实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public void inOrderTraversalByIterator(TreeNode root) {
    if (root == null) {
      return;
    }
    Stack<TreeNode> stack = new Stack<>();
    while (root != null || !stack.isEmpty()) {
      if (root != null) {
        // 不断将左节点的压栈
        stack.push(root);
        // 移动节点，将当前节点的左节点赋值给当前节点
        root = root.left;
      } else {
        // 移动到叶子节点，出栈
        // 例如第一次出栈 pop = 4, root = pop.right = null, 第二次出栈，pop = 5 ，打印5，root = pop.right = 8，
        // 然后8被入栈，再出栈打印，然后10 出栈， root = 19，然后 19 和 13 入栈，然后 13 出栈，19 出栈，24入栈，24 出栈 然后root == null, 栈为空
        TreeNode pop = stack.pop();
        // 打印或检查当前节点
        System.out.println(pop.val);
        // 将当前节点的右节点赋值给当前节点
        root = pop.right;
      }
    }
  }

中序遍历在leetcode中的应用

leetcode很多题目都是可以用中序来解题的，不过最常见的是利用中序依次从小到大输出的特性来解题，可以用来检查树是否符合二叉树要求

例如：98. Validate Binary Search Tree使用中序遍历以及定义一个前节点，判断前一个节点的值是否大于当前节点，还有99. Recover Binary Search Tree利用一个 pre 节点和当前节点比较，如果 pre 节点的值大于当前节点的值，那么就是我们要找的逆序的数字。分别用两个指针 first 和 second 保存即可。如果找到第二组逆序的数字，我们就把 second 更新为当前节点。最后把 first 和 second 两个的数字交换即可。

以及我们可以利用中序的特点加上前序或者后序来还原一棵树

例如：105. Construct Binary Tree from Preorder and Inorder Traversal和106. Construct Binary Tree from Inorder and Postorder Traversal就需要这样来解题，

由于篇幅有限，这里只是说一下，就不像上面一样详细的解题了，大家自己去尝试这解题，利用各种遍历的特性很容易就写出来的，leetcode中的Tree类型的难度普遍比动态规划和图要简单很多

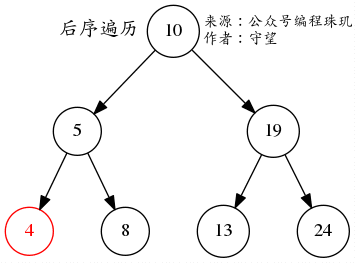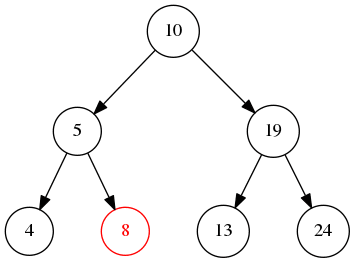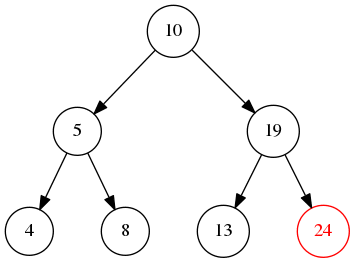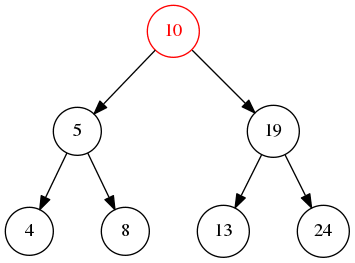
后序遍历

就是先递归遍历左右子树，然后检查当前节点值或者打印节点

1556505961545303

后序遍历会先遍历左再遍历右节点最后才是当前节点，所以，上图的输出是4->8->5->13->24->19->10，当然也可以反过来，那输出就是 24->13->19->8->4->5->10 这样子

递归写法

从左到右的方式

1
2
3
4
5
6
7
8
9
10
public void postOrderTraversalByRecursive(TreeNode root) {
    if (root != null) {
      // 递归左节点
      postOrderTraversalByRecursive(root.left);
      // 递归右节点
      postOrderTraversalByRecursive(root.right);
      // 打印当前节点
      System.out.println(root.val);
    }
  }

从右到左的方式

1
2
3
4
5
6
7
8
9
10
public void postOrderTraversalByRecursive(TreeNode root) {
    if (root != null) {
      // 递归右节点
      postOrderTraversalByRecursive(root.right);
      // 递归左节点
      postOrderTraversalByRecursive(root.left);
      // 打印当前节点
      System.out.println(root.val);
    }
  }

迭代写法

还是借助栈来实现入栈和出栈，同时我们还有定义一个last变量来保存上一个的值

从左到右的方式后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public void postOrderTraversalByIterator(TreeNode root) {
    Stack<TreeNode> stack = new Stack<>();
    // 定义上一个节点信息并初始化为空
    TreeNode last = null;
    while (root != null || !stack.isEmpty())
      if (root != null) {
        // 不断的将左边的数据压栈，并且移动节点将当前节点的左节点赋值给当前节点
        stack.push(root);
        root = root.left;
      } else {
        // 拿出栈顶的数据
        TreeNode peek = stack.peek();
        // 判断是否是有右节点，并且右节点不能等于上一个节点
        if (peek.right != null && peek.right != last) {
          root = peek.right;
        } else {
          // 出栈，并打印
          TreeNode pop = stack.pop();
          System.out.println(pop.val);
          // 将出栈的节点赋值给last，例如：第一次pop = 4，将 4 赋值给last，然后呢 这时候root还是 == null，这时候再次拿出栈顶元素5，
          // 而5有右节点，并且这时候last = 4， 所以root 会等于8，然后8入栈，然后出栈打印，这时候last = 8，root == null,
          // 下次这时候就应该要打印5了，而5是有右节点8的，但是我们刚刚好打印了8，并且把8赋值给了last，也就是说，5的右节点在上一次已经打印过了，我们可以直接打印5了，所以这时候我们只需要直接将5出栈并打印就可以了
          last = pop;
        }
      }
  }

从右到左的方式后序遍历

其实和上面一样，只是将root.left 换成root.right，peek.right 换成 peek.left而已

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public void postOrderTraversalByIterator(TreeNode root) {
   Stack<TreeNode> stack = new Stack<>();
   TreeNode last = null;
   while (root != null || !stack.isEmpty())
     if (root != null) {
       stack.push(root);
       // 更换的地方
       root = root.right;
     } else {
       TreeNode peek = stack.peek();
       // 更换的地方  
       if (peek.left != null && peek.left != last) {
         // 更换的地方
         root = peek.left;
       } else {
         TreeNode pop = stack.pop();
         System.out.println(pop.val);
         last = pop;
       }
     }
 }

修改前序遍历实现后序遍历

前序的输出10->5->4->8->19->13->24 而后序从右到左的输出是24->13->19->8->4->5->10，那么我们可以发现一个规律，后序的输出结果是前序输出结果的反转，那么从右到左的实现就可以改成将前序遍历的每个值放到集合中，然后反转整个集合即可

那么从左到右后序遍历我们只需要将root.right改为root.left，而root.left改为root.right即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public void preorderTraversal(TreeNode root) {
    Stack<TreeNode> stack = new Stack<>();
    List<Integer> result = new ArrayList<>();
    while (root != null || !stack.isEmpty()) {
      if (root != null) {
        result.add(root.val);
        stack.push(root);
        // 将root.left 改为 root.right
        root = root.right;
      }else {
        root = stack.pop();
        // 将root.right 改为 root.left
        root = root.left;
      }
    }
    // 反转集合元素
    Collections.reverse(result);
    result.forEach(System.out::println);
  }

后序遍历leetcode中的应用

leetcode中后序遍历的不太多，典型的从左到右大概就是145. Binary Tree Postorder Traversal后序遍历并将元素添加进集合就好了。还有结合中序遍历的106. Construct Binary Tree from Inorder and Postorder Traversal。

而从右到左遍历的有114. Flatten Binary Tree to Linked List，将二叉树变成链表形式的例子中，由于从左到右会出现有节点丢失的情况，所以我们逆着遍历就解决掉这个问题了，依次遍历 6 5 4 3 2 1，然后每遍历一个节点就将当前节点的右指针更新为上一个节点。

遍历到 5，把 5 的右指针指向 6。6 <- 5 4 3 2 1。

遍历到 4，把 4 的右指针指向 5。6 <- 5 <- 4 3 2 1。

因为更新当前的右指针的时候，当前节点的右孩子已经访问过了。而 6 5 4 3 2 1 的遍历顺序其实变形的后序遍历。

代码只需要将从右到左遍历的代码改一点点就可以了

1
2
3
4
5
6
7
8
9
10
if (peek.left != null && peek.left != last) {
  root = peek.left;
} else {
  TreeNode pop = stack.pop();
  // 将当前节点的右节点赋值为上一个节点，6->null, last = 6 ->null ,pop = 5, pop.r = last = 5->6->null,依次类推  
  pop.right = last;
  // 断开左边节点
  pop.left = null;
  last = pop;
}

BFS

BFS（广度优先遍历），在树结构中就是优先遍历每一层的节点，也就是层级遍历，在leetcode很多题目都能有BFS的解法。它能按层级顺序逐层的从左到右或者从右到左的输出每个节点，但是DFS其实也是可以按层输出的

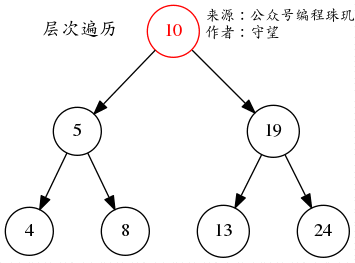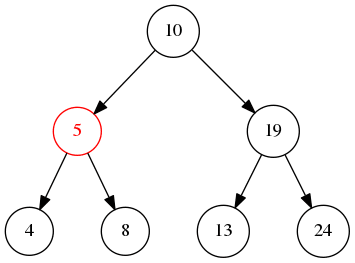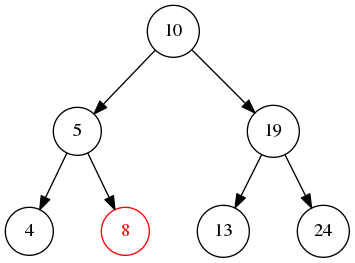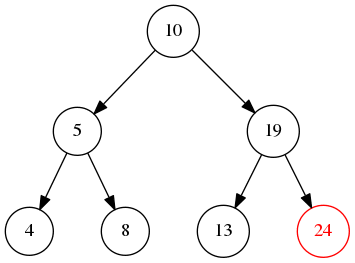
1556505962926865

如图所示我们将会输出10->5->19->4->8->13->24的结果

迭代方式

因为BFS不需要递归去遍历，而是借助队列(Queue)先进先出的方式来实现，所以我们就需要用到stack了，相比DFS，BFS会相对简单很多

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public void levelOrderTraversal(TreeNode root) {
    if (root == null) {
      return;
    }
    // 创建队列来保存节点
    Queue<TreeNode> queue = new LinkedList<>();
    // 将根节点存放进队列，队列第一轮存取 queue {10} 第二次 queue {5, 19} 第三次 {4， 8，13，24}
    queue.offer(root);
    while (!queue.isEmpty()) {
      // 获取队列长度
      int queueSize = queue.size();
      // 循环拿出队列的节点
      for (int i = 0; i < queueSize; i++) {
        // 拿出节点
        TreeNode pollNode = queue.poll();
        // 打印输出当前节点信息
        System.out.println(pollNode.val);
        // 判断左节点是否为空，不为空则存放进队列
        if (pollNode.left != null) {
          queue.offer(pollNode.left);
        }
        // 判断右节点是否为空，不为空则存放进队列
        if (pollNode.right != null) {
          queue.offer(pollNode.right);
        }
      }
    }
  }

BFS在leetcode中的应用

经典的就是将树的每一层放进集合中，例如：107. Binary Tree Level Order Traversal II直接BFS遍历整个树，for循环前创建一个内部集合，for循环后将内部集合放到结果集合中即可，还有一道也是类似的102. Binary Tree Level Order Traversal。

还有一道题是按照之字形添加进集合中的103. Binary Tree Zigzag Level Order Traversal。这道题也和上面类似，只不过定义一个level，level % 2 == 0 的情况下让内部集合往前插入数据 例如 insideList.add(0, root.val);

DFS 按层级放进集合

上面说到BFS在leetcode中的应用时，其实并不一定用BFS才能达到按层级划分的效果，DFS先序遍历其实也可以做到

我们只需要递归时传如一个level，然后并且list.size() 小于等于level时就new 一个内部集合即可，例如 :

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public void levelOrderTraversal(TreeNode root) {
    List<List<Integer>> result = new ArrayList<>();
    levelOrderTraversal(root, 0, result);
    result.forEach(list -> list.forEach(System.out::println));
  }

  private void levelOrderTraversal(TreeNode root, int level, List<List<Integer>> result) {
    if (root == null) {
      return;
    }
    // 集合长度小于等于层级，需要添加一个新年集合对象进去，不然后面result.get()会出现空指针
    if (result.size() <= level) {
      result.add(new ArrayList<>());
    }
    // 先序递归遍历，并且level + 1，注意不能使用++level
    result.get(level).add(root.val);
    levelOrderTraversal(root.left, level + 1, result);
    levelOrderTraversal(root.right, level + 1, result);
  }

同时我们也能用来解只能用BFS层级遍历来解的部分题目，例如：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public List<List<Integer>> zigzagLevelOrderByRecursiveDFS(TreeNode root) {
    List<List<Integer>> result = new ArrayList<>();
    zigzagLevelOrderByRecursiveDFS(root, 0, result);
    return result;
  }

  private void zigzagLevelOrderByRecursiveDFS(TreeNode root, int level, List<List<Integer>> result) {
    if (root == null) {
      return;
    }
    if (result.size() <= level) {
      result.add(new ArrayList<>());
    }
    if (level % 2 == 0) {
      result.get(level).add(root.val);
    } else {
      result.get(level).add(0, root.val);
    }
    zigzagLevelOrderByRecursiveDFS(root.left, level + 1, result);
    zigzagLevelOrderByRecursiveDFS(root.right, level + 1, result);
  }

Morris算法实现DFS

上面的那些遍历其实基本都能解大部分的题目，但是我们知道上面的实现，递归的话要出栈和入栈，迭代的话，要借助stack来保存节点来模拟入栈和出栈，那么空间复杂度肯定会有一定的损耗，空间复杂度基本上都是O(h)。

我们知道，左子树最后遍历的节点一定是一个叶子节点，它的左右孩子都是 null，我们把它右孩子指向当前根节点存起来，这样的话我们就不需要额外空间了。这样做，遍历完当前左子树，就可以回到根节点了，只更改节点指向我们就不需要借助栈了，空间复杂度也能达到一个常数级别O(1)

当然如果当前根节点左子树为空，那么我们只需要保存根节点的值，然后考虑右子树即可。

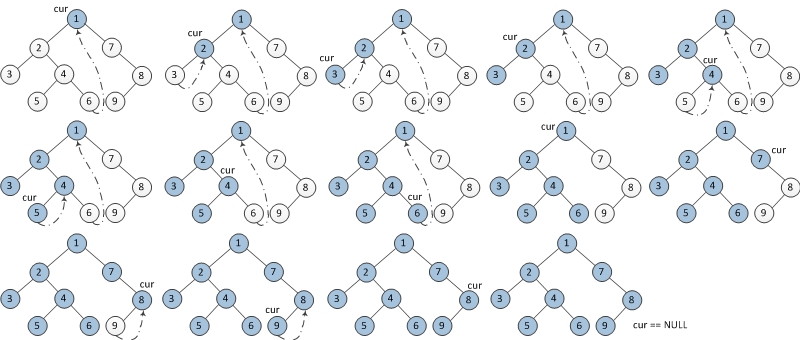
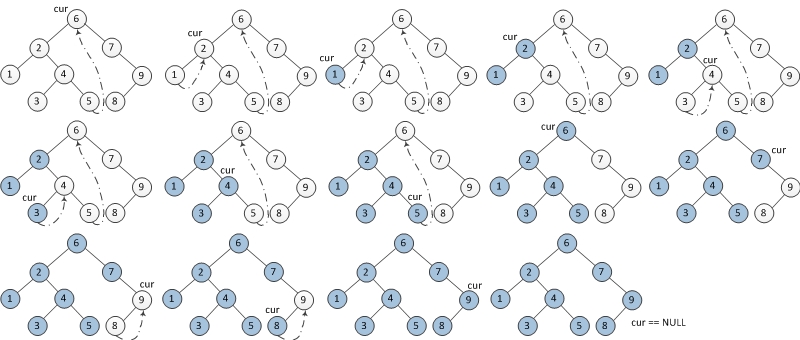
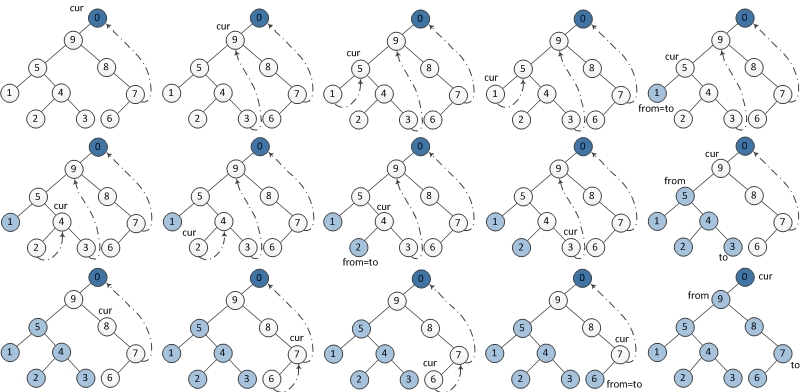
所以总体思想就是：记当前遍历的节点为 cur。

1、cur.left 为 null，保存 cur 的值，更新 cur = cur.right

2、cur.left 不为 null，找到 cur.left 这颗子树最右边的节点记做 last

2.1 pre.right 为 null，那么将 pre.right = cur，更新 cur = cur.left

2.2 per.right 不为 null，说明之前已经访问过，第二次来到这里，表明当前子树遍历完成，保存 cur 的值，更新 cur = cur.right

先序遍历

14221458-aa5f9e92cce743ccacbc735048133058

结合上面的总体思想和图片很容易就可以写出下面代码了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public void morrisPreOrderTravel(TreeNode root) {
   TreeNode cur = root;
   while (cur != null) {
     // 情况 1
     if (cur.left == null) {
       System.out.println(cur.val);
       cur = cur.right;
     } else {
       // 找左子树最右边的节点，同时右节点不能等于当前节点
       TreeNode pre = cur.left;
       while (pre.right != null && pre.right != cur) {
         pre = pre.right;
       }
       // 情况 2.1
       if (pre.right == null) {
         // 如果是2.1的情况就直接打印
         System.out.println(cur.val);
         pre.right = cur;
         cur = cur.left;
       }
       // 情况 2.2,第二次遍历节点
       if (pre.right == cur) {
         // 将前序节点的右节点恢复为空
         pre.right = null;
         cur = cur.right;
       }
     }
   }
 }

中序遍历

14214057-7cc645706e7741e3b5ed62b320000354

其实中序遍历和先序遍历代码几乎一样，只不过先序遍历的打印是在情况2.1的时候，而中序是情况2.2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public void morrisPreOrderTravel(TreeNode root) {
    TreeNode cur = root;
    while (cur != null) {
      // 情况 1
      if (cur.left == null) {
        System.out.println(cur.val);
        cur = cur.right;
      } else {
        //  找左子树最右边的节点，同时右节点不能等于当前节点
        TreeNode pre = cur.left;
        while (pre.right != null && pre.right != cur) {
          pre = pre.right;
        }
        // 情况 2.1
        if (pre.right == null) {
          pre.right = cur;
          cur = cur.left;
        }
        // 情况 2.2,第二次遍历节点
        if (pre.right == cur) {
          // 2.2 的情况就打印节点
          System.out.println(cur.val);
          pre.right = null;
          cur = cur.right;
        }
      }
    }
  }

后序遍历

我们上面在讲DFS 后序遍历时说过修改前序遍历实现后序遍历，那我们也可以用那种方式实现Morris的后序遍历，但是我们需要用一个集合来保存，但是这样就违背了我们想优化空间复杂度的初心了，所以我们会用另一种方式实现

贴一下代码，直接把所有的root.left 换成 root.right 还有 root.right 换成root.left 即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public void morrisPreOrderTravel(TreeNode root) {
    TreeNode cur = root;
    List<Integer> result = new ArrayList<>();
    while (cur != null) {
      // 情况 1
      if (cur.right == null) {
        result.add(cur.val);
        cur = cur.left;
      } else {
        //  找左子树最右边的节点，同时右节点不能等于当前节点
        TreeNode pre = cur.right;
        while (pre.left != null && pre.left != cur) {
          pre = pre.left;
        }
        // 情况 2.1
        if (pre.left == null) {
          result.add(cur.val);
          pre.left = cur;
          cur = cur.right;
        }
        // 情况 2.2,第二次遍历节点
        if (pre.left == cur) {
          pre.left = null;
          cur = cur.left;
        }
      }
    }
    Collections.reverse(result);
    result.forEach(System.out::println);
  }

ok，会到正题，Morris的后序相对前面的两个要难实现很多，需要建立一个临时节点 dump，令其左孩子是 root。并且还需要一个子过程，就是倒序输出某两个节点之间路径上的各个节点。

步骤：

当前节点设置为临时节点 dump。

  1. 如果当前节点的左孩子为空，则将其右孩子作为当前节点。

  2. 如果当前节点的左孩子不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点。

    1. 如果前驱节点的右孩子为空，将它的右孩子设置为当前节点。当前节点更新为当前节点的左孩子。
    2. 如果前驱节点的右孩子为当前节点，将它的右孩子重新设为空。倒序输出从当前节点的左孩子到该前驱节点这条路径上的所有节点。当前节点更新为当前节点的右孩子。

  3. 重复以上 1、2 直到当前节点为空。

15165951-7991525829134fb3beefed9fbf7e0536

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
public void postOrderMorrisTraversal(TreeNode root) {
    TreeNode dump = new TreeNode(0);
    dump.left = root;
    TreeNode cur = dump;
    while (cur != null) {
      // 情况 1
      if (cur.left == null) {
        cur = cur.right;
      } else {
        // 找左子树最右边的节点
        TreeNode pre = cur.left;
        while (pre.right != null && pre.right != cur) {
          pre = pre.right;
        }
        // 情况 2.1
        if (pre.right == null) {
          pre.right = cur;
          cur = cur.left;
        }
        // 情况 2.2,第二次遍历节点
        if (pre.right == cur){
          // 与其他三种遍历不同的地方，反转打印，图中的1-1、2-2、5-3、6-6、9-7
          printReverse(cur.left, pre);
          pre.right = null;
          cur = cur.right;
        }
      }
    }
  }

  private void printReverse(TreeNode from, TreeNode to) {
    // 将to 变成 form的反转节点 例如 from为5.right->4.r->3.r->9.r->.... to为3.right->9.r->8.r->...
    // 反转完，form的根节点还是5，from = 5.r->4.r->5.r->4.r->5.r->... to为from刚刚反转后的内容to = 3.r->4.r->5.r->4.r->...
    reverse(from, to, from.right);
    // 用一个临时遍历来保存to，并不断右移
    TreeNode tempNode = to;
    while (true) {
      // 打印to的内容，例如第一次，3，第二次，4，第三次，5
      System.out.println(tempNode.val);
      // 为了保证不会死循环打印下去，所以当to移到from的节点也就是5时，就结束掉整个循环
      if (tempNode == from) {
        break;
      }
      // 不断右移
      tempNode = tempNode.right;
    }
    // 将to 变成 from 的反转节点，反转后 from = 5.r->4.r->3.r->4.r->3.r->.... to = 3.r->4.r->3.r->4.r->....
    reverse(to, from, from.right);
  }

  private void reverse(TreeNode from, TreeNode to, TreeNode fromRight) {
    // 如果都是同一个节点的情况，例如图中的1，2，6
    if (from == to) {
      return;
    }
    // 遍历并反转
    do {
      TreeNode temp = fromRight.right;
      fromRight.right = from;
      from = fromRight;
      fromRight = temp;
    } while (from != to);
  }

总结

除了Morris实现DFS有点复杂之外，其他的都是比较基础的知识，掌握这些遍历的方式，对逻辑思维锻炼很有帮助，刷跟树有关的算法也会发现轻松很多。建议大家多刷leetcode，并且尝试用不同的遍历方式去解题，多刷题真的很难锻炼思维能力，也会成长的更快。

由于篇幅和时间紧迫问题，本文写的比较粗略和不完善，也可能存在一定的错误，有错误的地方，希望大家可以在底下评论给我留言，让我这个小白有机会认识到自己的错误并且改正

参考资料

动画：二叉树遍历的多种姿势

Morris Traversal 方法遍历二叉树（非递归，不用栈，O(1)空间

leetcode

Author：tobias

原文链接：http://tobiasll.github.io/2019/11/26/二叉树DFS、BFS、Morris遍历/

发表日期：November 26th 2019, 2:46:16 pm

更新日期：November 29th 2019, 9:31:30 am

版权声明：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. 序言
  2. 2. DFS
    1. 2.1. 前序遍历
      1. 2.1.1. 递归写法
      2. 2.1.2. 迭代写法
        1. 2.1.2.1. 第一种，丢失右节点
        2. 2.1.2.2. 第二种，不丢失右节点
      3. 2.1.3. 两种遍历在leetcode的应用
    2. 2.2. 中序遍历
      1. 2.2.1. 递归写法
      2. 2.2.2. 迭代写法
      3. 2.2.3. 中序遍历在leetcode中的应用
    3. 2.3. 后序遍历
      1. 2.3.1. 递归写法
        1. 2.3.1.1. 从左到右的方式
        2. 2.3.1.2. 从右到左的方式
      2. 2.3.2. 迭代写法
        1. 2.3.2.1. 从左到右的方式后序遍历
        2. 2.3.2.2. 从右到左的方式后序遍历
        3. 2.3.2.3. 修改前序遍历实现后序遍历
      3. 2.3.3. 后序遍历leetcode中的应用
  3. 3. BFS
    1. 3.0.1. 迭代方式
    2. 3.0.2. BFS在leetcode中的应用
  • 4. DFS 按层级放进集合
  • 5. Morris算法实现DFS
    1. 5.1. 先序遍历
    2. 5.2. 中序遍历
    3. 5.3. 后序遍历
  • 6. 总结
  • 7. 参考资料
    • Total : 6
    2019
    MySQL jvm 工具使用 数据结构与算法